Poor man's Lorenz Attractor

References/links:

• The schematic from The Art of Electronics
• My schematic (pdf)
• Another implementation from Glen's Stuff
• Wikipedia entry

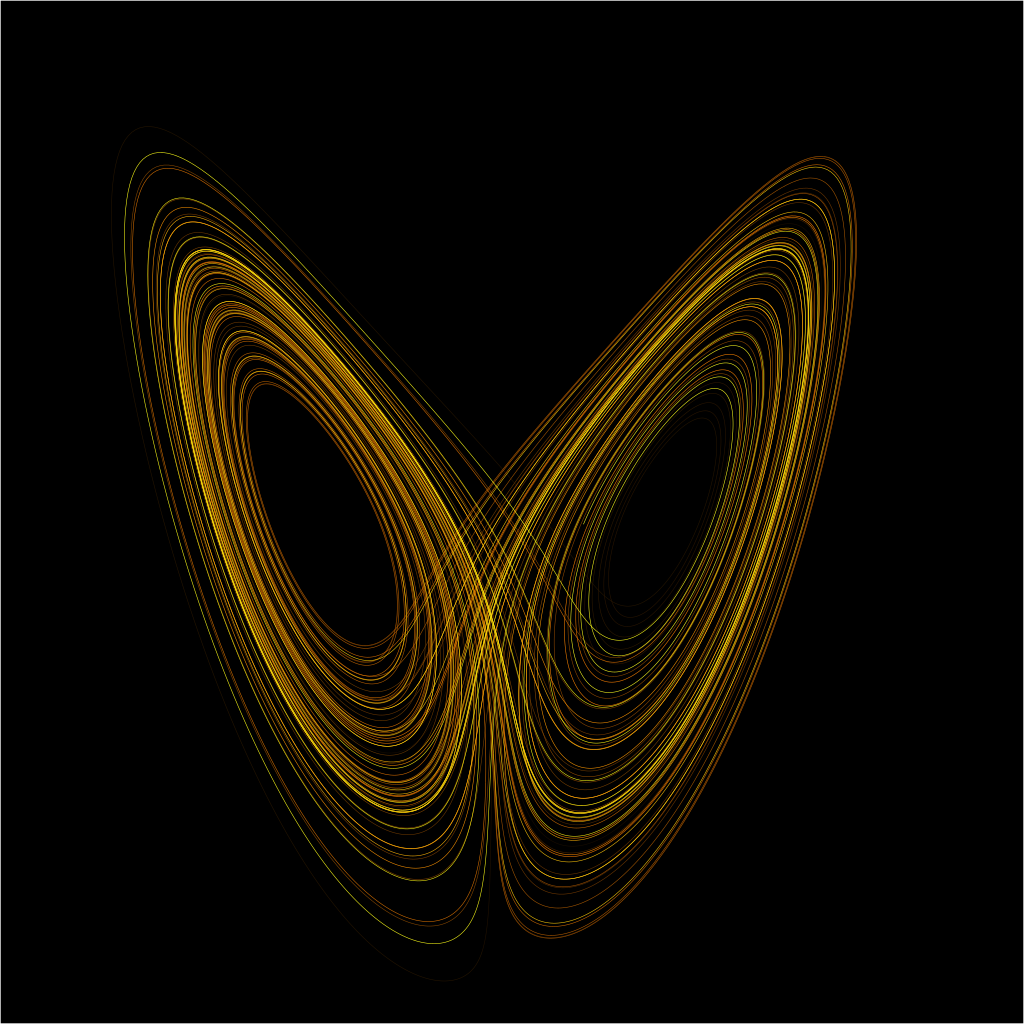
The first time I came across the Lorenz attractor was in the book Chaos: Making a New Science. That was in 1996 (I was in high school back then). It is a system of three simple differential equations that exhibit a very complex behavior.

The Lorenz system: $${dx \over dt} = \sigma (y-x)$$ $${dy \over dt} = \rho x-y-xz$$ $${dz \over dt} = xy - \beta z$$ Parameter values: \(\sigma=10\), \(\beta={8 \over 3}\), \(\rho=28\).

I recently saw a circuit that solves Lorenz's differential equations in The Art of Electronics: The x Chapters. So I thought "great, let's do it". But then I found out how much the MPY634 multiplier costs. Almost $24 in Digikey. And you need two of them.

So what are the alternatives? The cheapest multiplier in stock was AD633. The difference between the two is mainly their precision (0.5% vs 2%). Guess what costs what. Would it work with ±2% error? (Spoiler: it does). And why not go dirt cheap with an LM324 op amp? This is the circuit I came up with:

The breadboard circuit has a couple of components more than the schematic. I omitted them for the sake of simplicity. The 10-turn pot in series with a \(330k\) resistor makes \(R_7\) as close to \(374k\) as possible. The jumpers short-circuit the inputs of \(U_1\) and \(U_2\) to ground in order trim their offset.

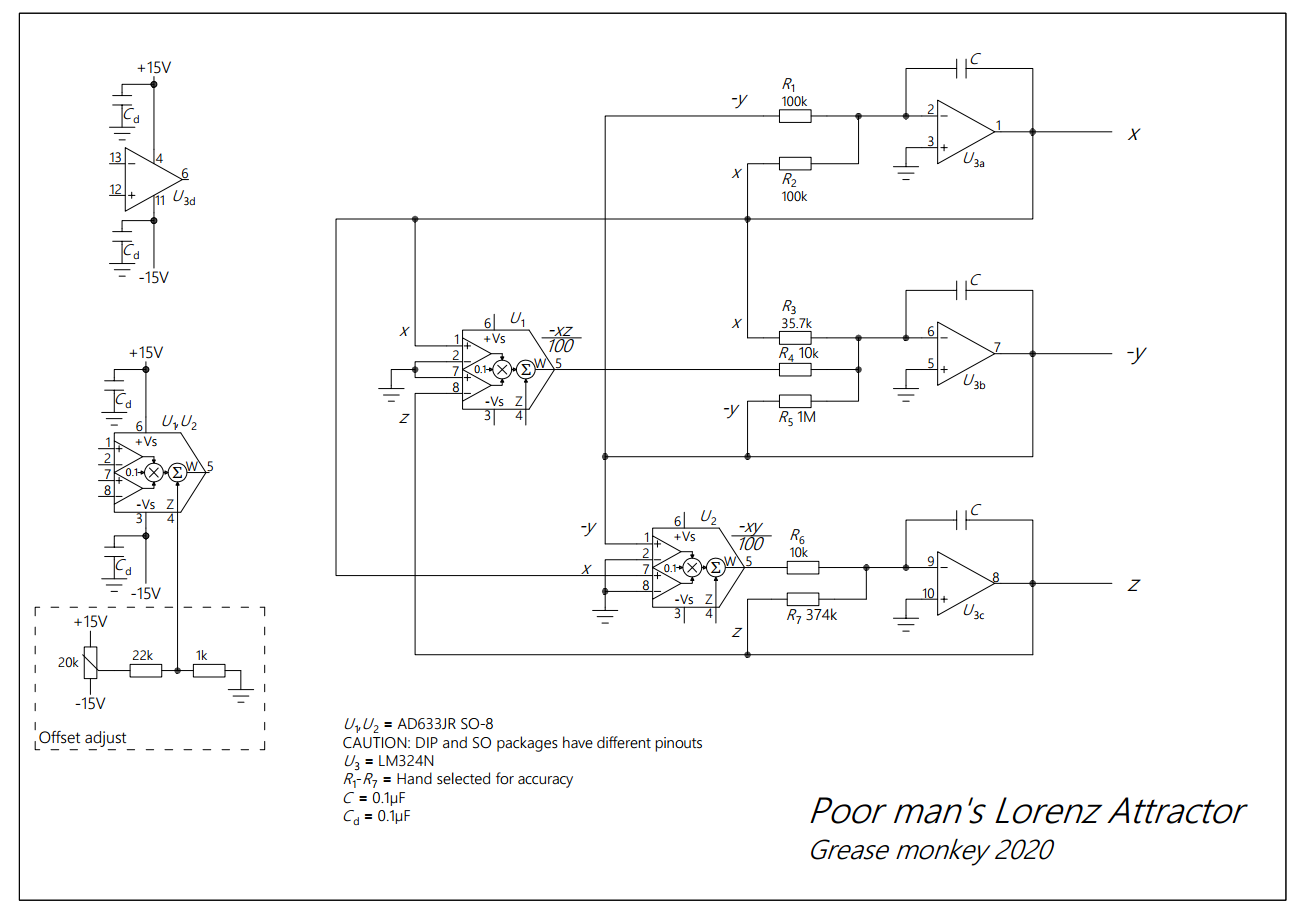
If you need the circuit to run at a different speed change the values of C. Smaller capacitors make it run faster. After some tries I found out that for my humble DS1052E 0.1μF is fine.

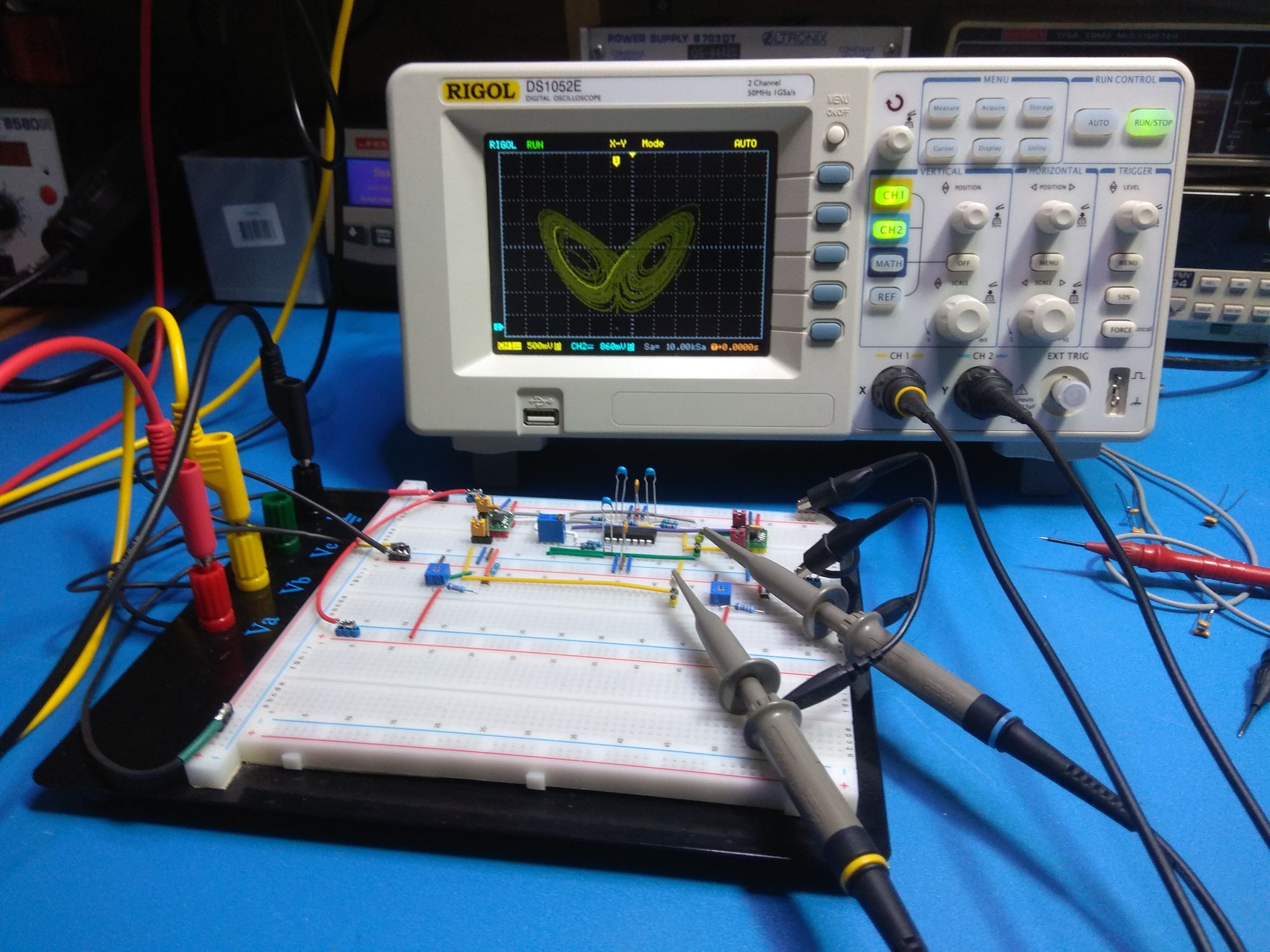
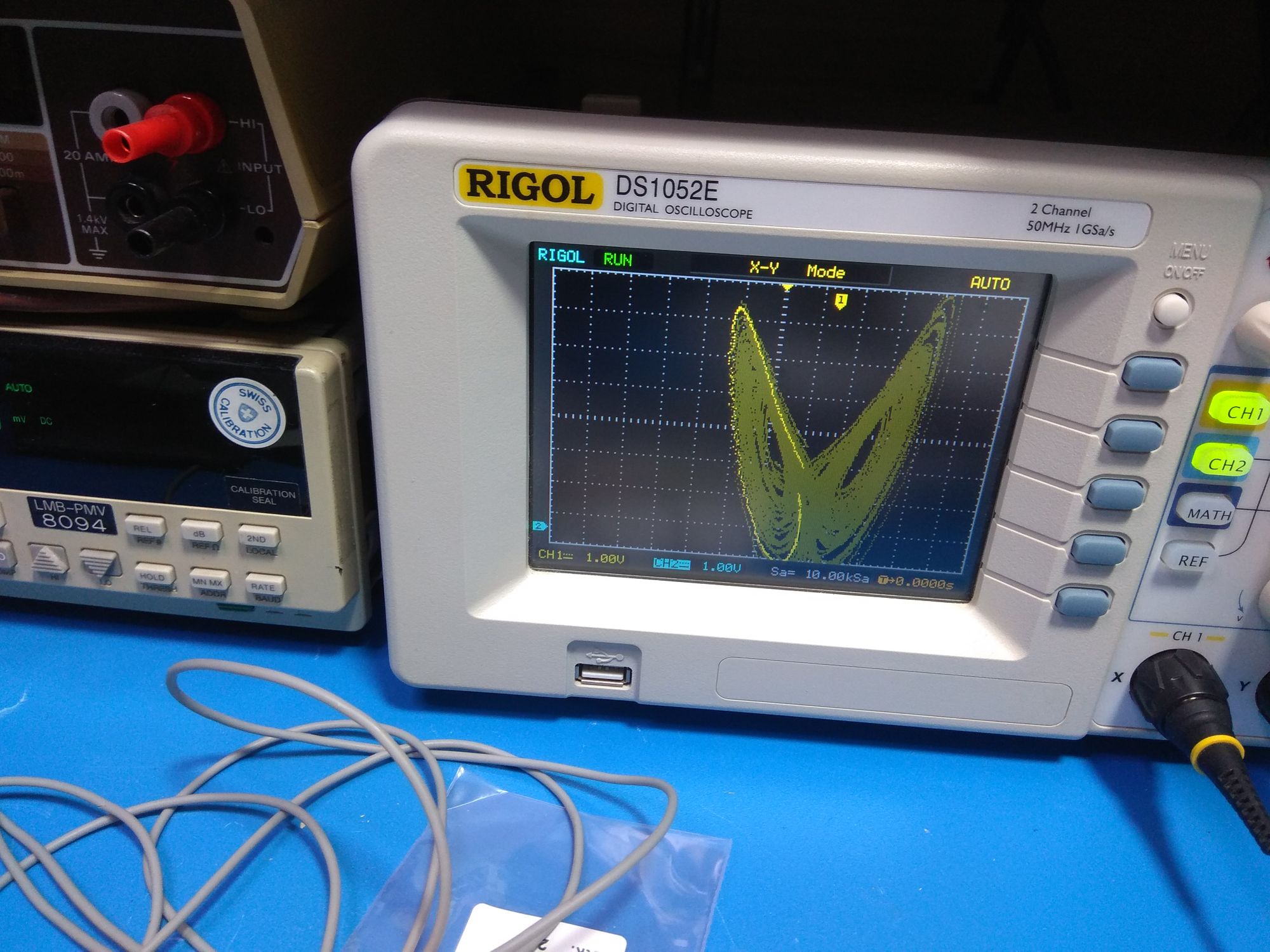
Update 16.06.2020

I just got a new oscilloscope. So here's a video of the circuit's output.