References/links:
LXI is a communication protocol for instrumentation. It allows various instruments to work together. Something like GPIB over Ethernet. LXI uses the VXI-11 interface.
Test connection
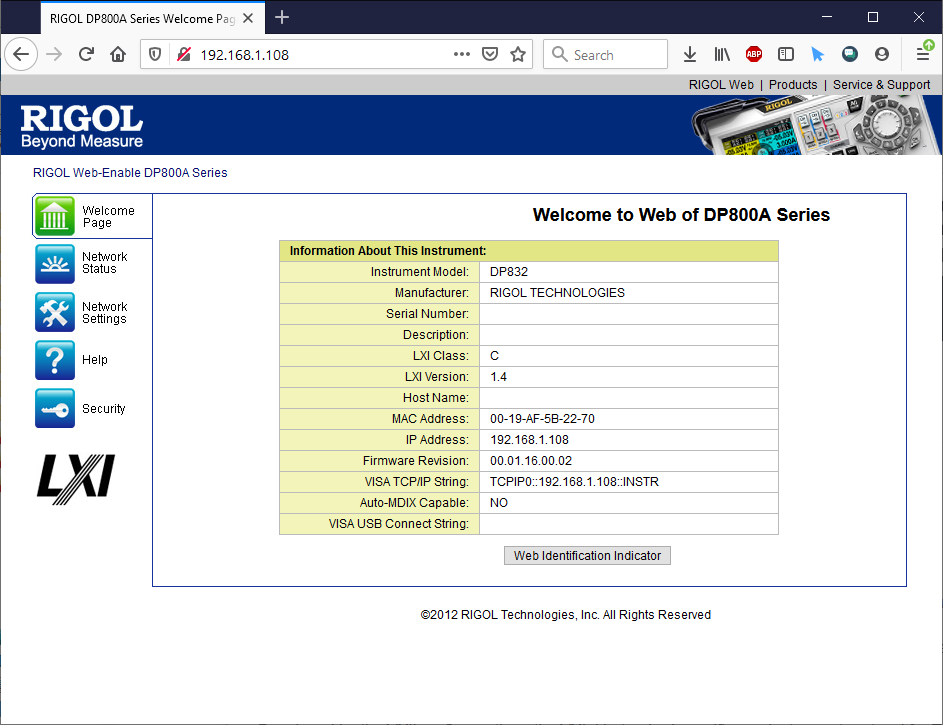
First find out what your IP is. Press Utility I/O Config LAN. You should see the IP now. Mine is 192.168.1.108.

To test the connection from your computer type the IP address in a browser. You should see a web page.
Python test
To test the connectivity with python run the following program. It sends the *IDN? command.
If all is good you should see the reply:
RIGOL TECHNOLOGIES,DP832,[Serial number],00.01.16
Useful LXI commands for the DP800 Series
These command are just to whet your appetite. For the full set of commands consult the DP800 Series Programming Guide.
Channel specific commands:
- Set the voltage of CH1 to 10.512 V
:SOURce1:VOLT 10.512 - Read the output voltage of CH1
MEAS:VOLT? CH1 - Read the voltage set-point of CH1
:SOUR1:VOLT? - Set the current of CH1 to
:SOUR1:CURR 1.321 - Read the output current of CH1
MEAS:CURR? CH1 - Read the current set-point of CH1
:SOUR1:CURR? - Read the output power of CH1
MEAS:POWE? CH1 - Turn CH1 on
:OUTP CH1,ON - Turn CH1 off
:OUTP CH1,OFF
System commands:
- Turn system lock on
:SYST:RWL ON - Turn system lock off
:SYST:RWL OFF - Read the heat-sink temperature
:SYSTem:SELF:TEST:TEMP? - Turn all chanels on
:OUTP ALL,ON - Turn all chanels off
:OUTP ALL,OFF
Python example
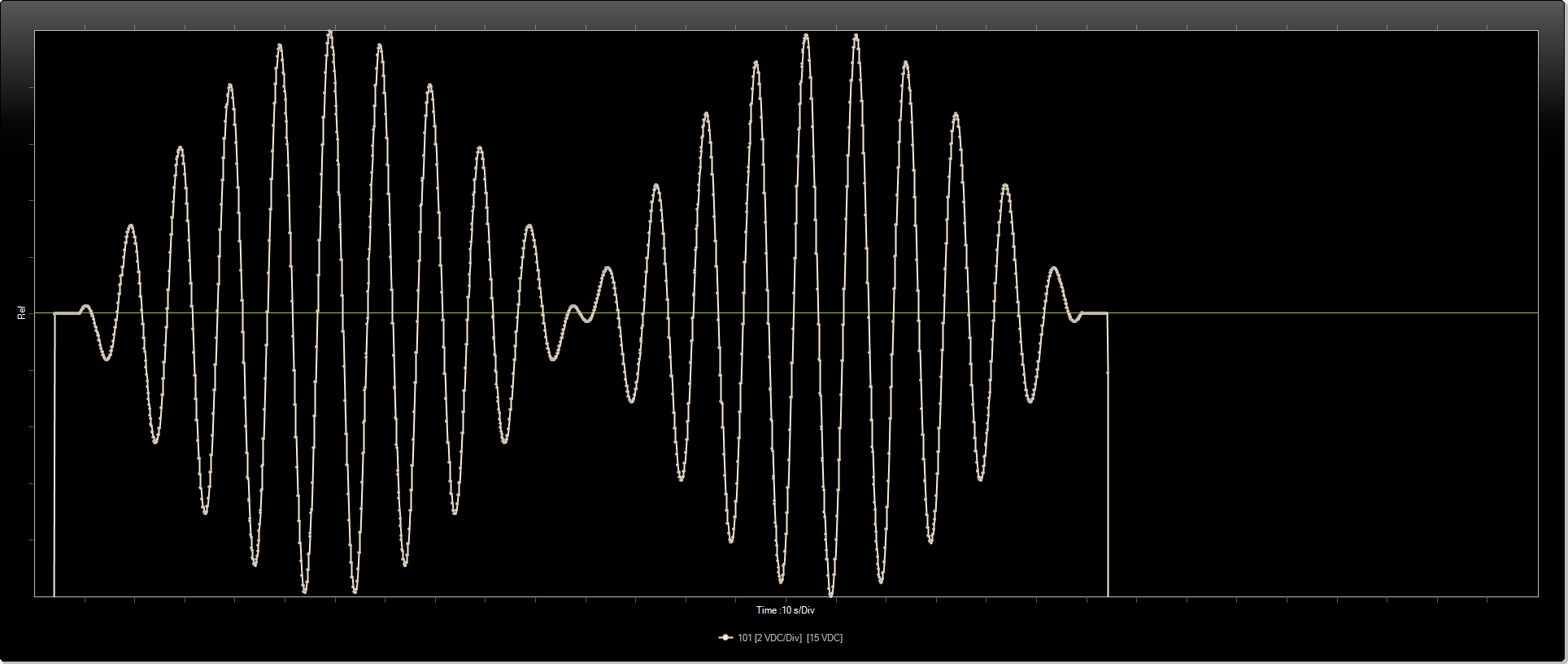
Now let's make the DP832 do something funny. The output is capture by a HP34970A (5.5 digits, ±100VDC, 1 PLC, every 100ms) and BenchLink Data Logger 3.
This is the output: